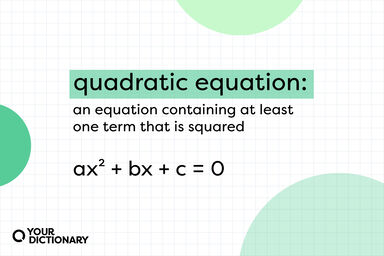Equation Definition
ĭ-kwāzhən, -shən
equations
noun
equations
The act of equating; equalization.
Webster's New World
The state of being equal.
American Heritage
The state of being equated; equality, equivalence, or balance; also, identification or association.
Webster's New World
A complex whole.
The human equation.
Webster's New World
A statement of equality between two quantities, as shown by the equal sign (=)
A quadratic equation.
Webster's New World
Synonyms:
- par
- equivalence
- equality
- equating
- formal statement of equivalence
- mathematical statement
- equalization
- comparison
- sameness
- parity
- equivalency
Other Word Forms of Equation
Noun
Singular:
equationPlural:
equationsOrigin of Equation
-
From Old French, from Latin aequātiō (“an equalizing”).
From Wiktionary
Find Similar Words
Find similar words to equation using the buttons below.