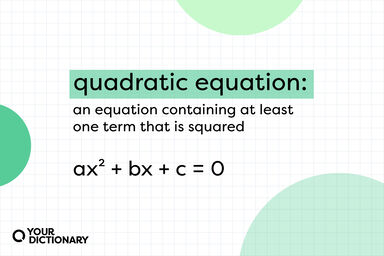Conversely, if the kinetic energy T is expressed as a quadratic function of x, x x3, y1, y2, y3, the components of momentum, the partial differential coefficient with respect to a momentum component will give the component of velocity to correspond.
Thus if T is expressed as a quadratic function of U, V, W, P, Q, R, the components of momentum corresponding are dT dT dT (I) = dU + x2=dV, x3 =dW, dT dT dT Yi dp' dQ' y3=dR; but when it is expressed as a quadratic function of xi, 'x2, x3, yi, Y2, Y3, U = d, V= dx, ' w= ax dT Q_ dT dT dy 1 dy2 dy The second system of expression was chosen by Clebsch and adopted by Halphen in his Fonctions elliptiques; and thence the dynamical equations follow X = dt x2 dy +x3 d Y = ..., Z ..., (3) = dt1 -y2?y - '2dx3+x3 ' M =..
It follows from §§ 48 and 51 that, if V is a solid figure extending from a plane K to a parallel plane L, and if the area of every cross-section parallel to these planes is a quadratic function of the distance of the section from a fixed plane parallel to them, Simpson's formula may be applied to find the volume of the solid.
In the case of the sphere, for instance, whose radius is R, the area of the section at distance x from the centre is lr(R 2 -x 2), which is a quadratic function of x; the values of So, Si, and S2 are respectively o, 7rR 2, and o, and the volume is therefore s.
By drawing Ac and Ad parallel to BC and BD, so as to meet the plane through CD in c and d, and producing QP and RS to meet Ac and Ad in q and r, we see that the area of Pqrs is (x/h - x 2 /h 2) X area of cCDd; this also is a quadratic function of x.