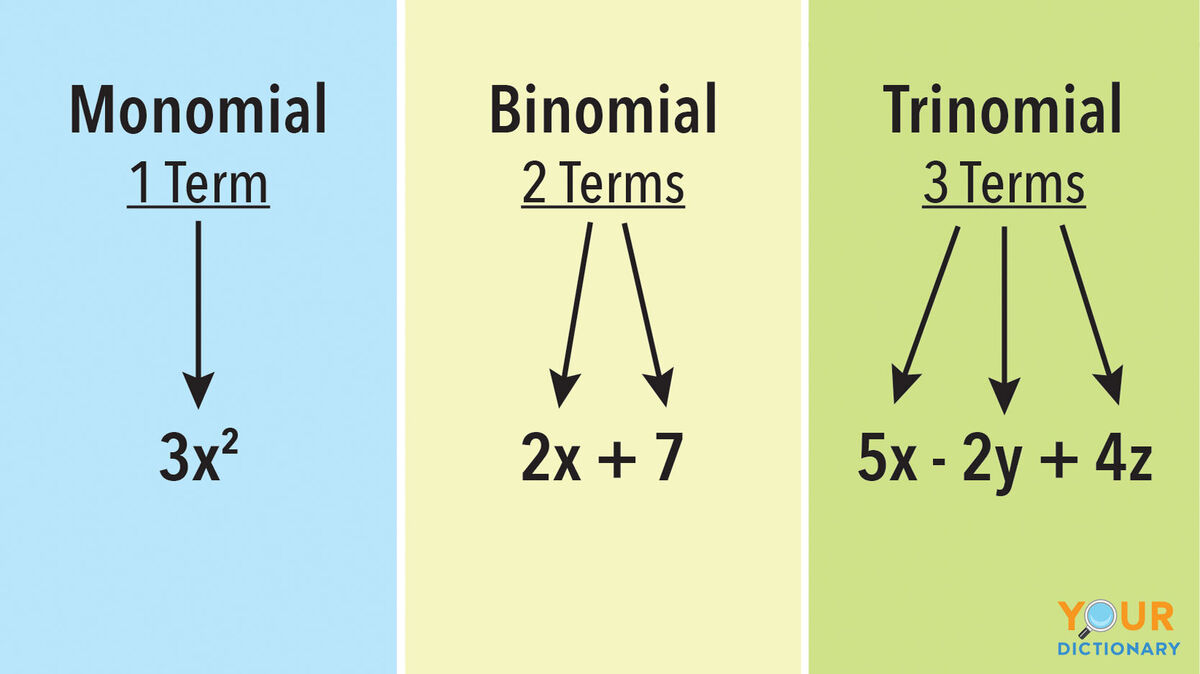
A monomial is an expression in algebra that contains one term, like 3xy. Monomials include numbers, whole numbers and variables that are multiplied together, and variables that are multiplied together. A polynomial is a sum of monomials where each monomial is called a term. Read more about the difference between monomials and polynomials, the rules for each term and several helpful examples.
Identifying a Monomial
Finding a monomial is easier than it seems. "Mono" means one, meaning that "monomial" includes only one term. It is a piece of a polynomial. Monomials can include these characteristics:
- any number by itself (such as 5, 2700 or 83)
- a variable (such as "b" or "x")
- a coefficient that multiplies the variable (such as the 4 in "4x")
- positive exponents (such as the 2 in 7x2)
- a combination of these (such as 98b or 78xyz)
Monomials cannot have a fractional or negative exponent. Monomial examples include:
- 6xy3
- 948
- 2y3z2
- a2
- -7b
- y
- 36
- -12x
- a8b4c2
- 72a
A monomial multiplied by a monomial is also a monomial. A monomial multiplied by a constant (not variable) is also a monomial. When looking at examples of monomials, you need to understand different types of polynomials, which have more than one term (since "poly" means "many.") Following is an explanation of polynomials, binomials, trinomials, and degrees of a polynomial.
Identifying a Polynomial
A polynomial shows the sum of monomials. It is an algebraic expression with a finite number of terms. Because a polynomial is made of monomials, it also cannot have negative exponents.
Polynomial examples include:
- 7a2 + 18a - 2
- -2x5 + 17x3 - 9x
- 5a - 12
- 6m4 - 3n
- 11x2 + 3b − 4b3 + 10
- x - y
- 8a5 - 7a
- -2x9 + x3 + x2
- 12a + 14b
- 9 + 9a2
Types of Polynomials
If you notice that these polynomials have different terms, that's because they're different types of polynomials.
- binomials - a polynomial with two terms (such as in 3x + 1 and 2 - 5x)
- trinomials - a polynomial with three terms (such as 2x2 + 4x - 11 and 4x3 - 13x + 9)
When a polynomial has four terms (such as 5x6 - 17x2 + 97 + 24x), it's sometimes called a quadrinomial. However, larger polynomials are usually known as four-term polynomials, five-term polynomials, and so on.
Degrees of Monomials and Polynomials
The degree of a monomial or polynomial is the highest power of the variable in that polynomial, as long as there is only one variable. If there is more than one variable, you add up the exponents for all the variables to find the degree.
If a polynomial has more than one variable, then you can find the degree of by looking at each monomial. For example: 14x4 + 27x2y - y has the degree of 4. Looking at each individual term, you find that the exponents are 4, 3 (2+implicit 1), and 1). 4 is the highest, so the degree is 4.
For example:
- The degree of the monomial 8xy2 is 3, because x has an implicit exponent of 1 and y has an exponent of 2 (1+2 = 3).
- The degree of the polynomial 7x3 - 4x2 + 2x + 9 is 3, because the highest power of the only variable x is 3.
- The degree of the polynomial 18s12 - 41s5 + 27 is 12. There is one variable (s) and the highest power of s here is 12.
- The degree of the polynomial 8z + 2008 is 1, because z is the only variable and is in the first power.
Degrees of Polynomial Terms
A second degree polynomial (such as 6x2 + 13x + c) is also called a “quadratic.” You may wonder where the word “quadratic” comes from, because the prefix “quad” usually stands for four. The word comes from the Latin word for “making square.” So, in this instance, “quad” refers to the four corners of a square. A third degree polynomial is called a “cubic”, a fourth degree is called a "quartic", and a fifth degree polynomial is called a "quintic." Sixth degree polynomials are "sextic" and seventh degree polynomials are "septic."
Algebra Means Restoration
Algebra, which is Arabic for "restoration," is a branch of pure mathematics. Pure mathematics differs from other disciplines because it is not necessarily applied to any particular situation, but it investigates the concepts and beauty of math itself. The history of algebra is enriching as well; from the ancient mathematical tablets of Babylon to the classical days of Diophantus, Greek mathematician and writer of Arithmetica, and the Medieval discovery of algebra itself by the "father of algebra," Al-Khwarizmi (whose name was the inspiration for the word algorithm.), algebra is a way to bring balance to mathematics.