Binomial Theorem Definition

noun
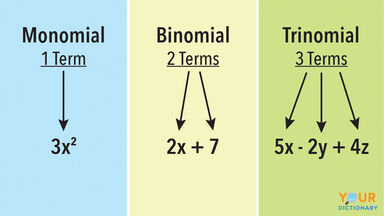
The theorem that specifies the expansion of any power ( a + b ) m of a binomial ( a + b ) as a certain sum of products aibj , such as ( a + b )2 = a2 + 2 ab + b2 .
American Heritage
The general formula for the expansion of any binomial when raised to a power that is a positive whole number; the expansion of (a + b)n: discovered by Omar Khayyám and generalized by Sir Isaac Newton (Ex.: (a + b)2 = a2 + 2ab + b2)
Webster's New World

(mathematics) A formula giving the expansion of a binomial such as raised to any positive integer power, i.e. . It's possible to expand the power into a sum of terms of the form where the coefficient of each term is a positive integer. For example.

Wiktionary

Binomial Theorem Sentence Examples

  • With Descartes the use of exponents as now employed for denoting the powers of a quantity becomes systematic; and without some such step by which the homogeneity of successive powers is at once recognized, the binomial theorem could scarcely have been detected.

  • The binomial theorem gives a formula for writing down the coefficient of any stated term in the expansion of any stated power of a given binomial.

  • This is the binomial theorem for a positive integral index.

  • The binomial theorem for positive integral index may then be written (x + y) n = -iyi +.

  • If we represent this expression by f (x), the expression obtained by changing x into x-+-h is f(x+h); and each term of this may be expanded by the binomial theorem.

More Sentences

Related Articles

Find Similar Words

Find similar words to binomial theorem using the buttons below.

Words Starting With

BBIBIN

Words Ending With

MEMREM

Unscrambles

binomial theorem

Words Starting With B and Ending With M

Starts With B & Ends With MStarts With BI & Ends With MStarts With B & Ends With EM

Word Length