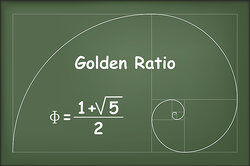
The intercept on the axis of y is 2a/7r; therefore, if it were possible to accurately construct the curve, the quadrature of the circle would be effected.
Montucla, successful attempt to show that quadrature of the circle by a Euclidean construction was impossible.'
He attempted the quadrature of the circle by interpolation, and arrived at the remarkable expression known as Wallis's Theorem (see Circle, Squaring Of).
Rectification and quadrature of the circle have thus been, since the time of Archimedes at least, practically identical problems. Again, since the circumferences of circles are proportional to their diameters - a proposition assumed to be true from the dawn almost of practical geometry - the rectification of the circle is seen to be transformable into finding the ratio of the circumference to the diameter.
He is described as the first to treat theology on mathematical principles and he also wrote on the quadrature of the circle.