scalar

(skā′lər)

adjective

in, on, or involving a scale or scales
Math. designating or of a quantity that has magnitude but no direction in space, as volume or temperature

Origin: L scalaris, of a ladder < scalae, steps, ladder: see scale

noun

a scalar quantity

See scalar in American Heritage Dictionary 4

noun

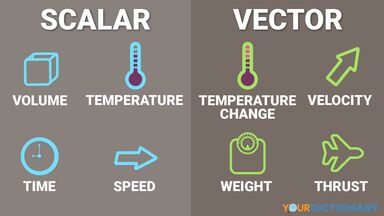
a. A quantity, such as mass, length, or speed, that is completely specified by its magnitude and has no direction.
b. Mathematics A number, numerical quantity, or element in a field.
A device that yields an output equal to the input multiplied by a constant, as in a linear amplifier.

adjective

Of or relating to a scalar.

Origin:

Origin: Latin scālāris, of a ladder

Origin: , from scālae, ladder; see Scale ²

Learn more about scalar

scalar computer definition

scalar science

scalar in a sentence

Related Articles

Examples of Vector and Scalar Quantity in Physics