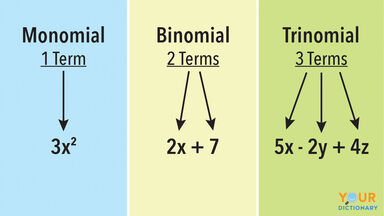
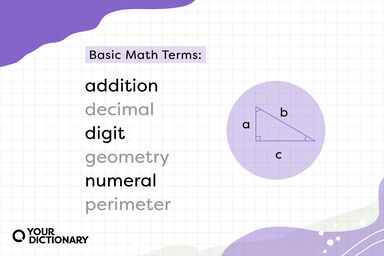
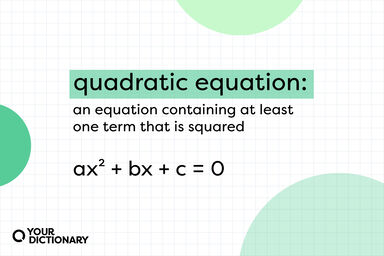Algebra Definition
Other Word Forms of Algebra
Noun
Origin of Algebra
-
Middle English bone-setting and Italian algebra both from Medieval Latin from Arabic al-jabr (wa-l-muqābala) the restoration (and the compensation), addition (and subtraction) al- the jabr bone-setting, restoration (from jabara to set (bones), force, restore gpr in Semitic roots)
From American Heritage Dictionary of the English Language, 5th Edition
-
From Medieval Latin, from Arabic word الجبر (al-jabr, “reunion, resetting of broken parts”) in the title of al-Khwarizmi's influential work الكتاب المختصر في حساب الجبر والمقابلة (al-kitāb al-muxtaṣar fī ḥisāb al-jabr wa-l-muqābala, “The Compendious Book on Calculation by Completion and Balancing”).
From Wiktionary
Find Similar Words
Find similar words to algebra using the buttons below.