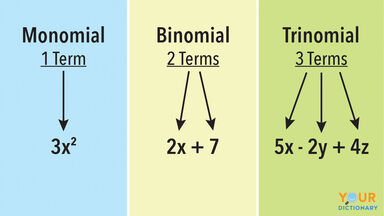
Monomial Definition

mŏ-nōmē-əl, mə-
noun
A monomial expression, quantity, or name.
Webster's New World
A taxonomic name consisting of a single word.
American Heritage Medicine
Advertisement
adjective
Consisting of only one term.
Webster's New World
Consisting of only one word.
Webster's New World
Advertisement

Other Word Forms of Monomial

Noun

Singular:
monomial
Plural:
monomials

Origin of Monomial

  • Syncopic form of mononomial.

    From Wiktionary

  • mon(o)– (bin)omial

    From American Heritage Dictionary of the English Language, 5th Edition

Monomial Sentence Examples

  • The general monomial symmetric function is a P1 a P2 a P3.

  • Since dp4+(-)P+T1(p +q qi 1)!dd4, the solutions of the partial differential equation d P4 =o are the single bipart forms, omitting s P4, and we have seen that the solutions of p4 = o are those monomial functions in which the part pq is absent.

  • In order that a monomial containing a m as a factor may be divisible by a monomial containing a p as a factor, it is necessary that p should be not greater than m.

  • A finite group G is called monomial (or M -group) if each ordinary irreducible character of G is monomial.

  • A separation is the symbolic representation of a product of monomial symmetric functions.

More Sentences

Related Articles

Advertisement

Find Similar Words

Find similar words to monomial using the buttons below.

Words Starting With

MMOMON

Words Ending With

LALIAL

Unscrambles

monomial

Words Starting With M and Ending With L

Starts With M & Ends With LStarts With MO & Ends With LStarts With M & Ends With AL

Word Length

8 Letter Words8 Letter Words Starting With M8 Letter Words Ending With L