Random sampling is a statistical technique used in selecting people or items for research. There are many techniques that can be used. Each technique makes sure that each person or item considered for the research has an equal opportunity to be chosen as part of the group to be studied.
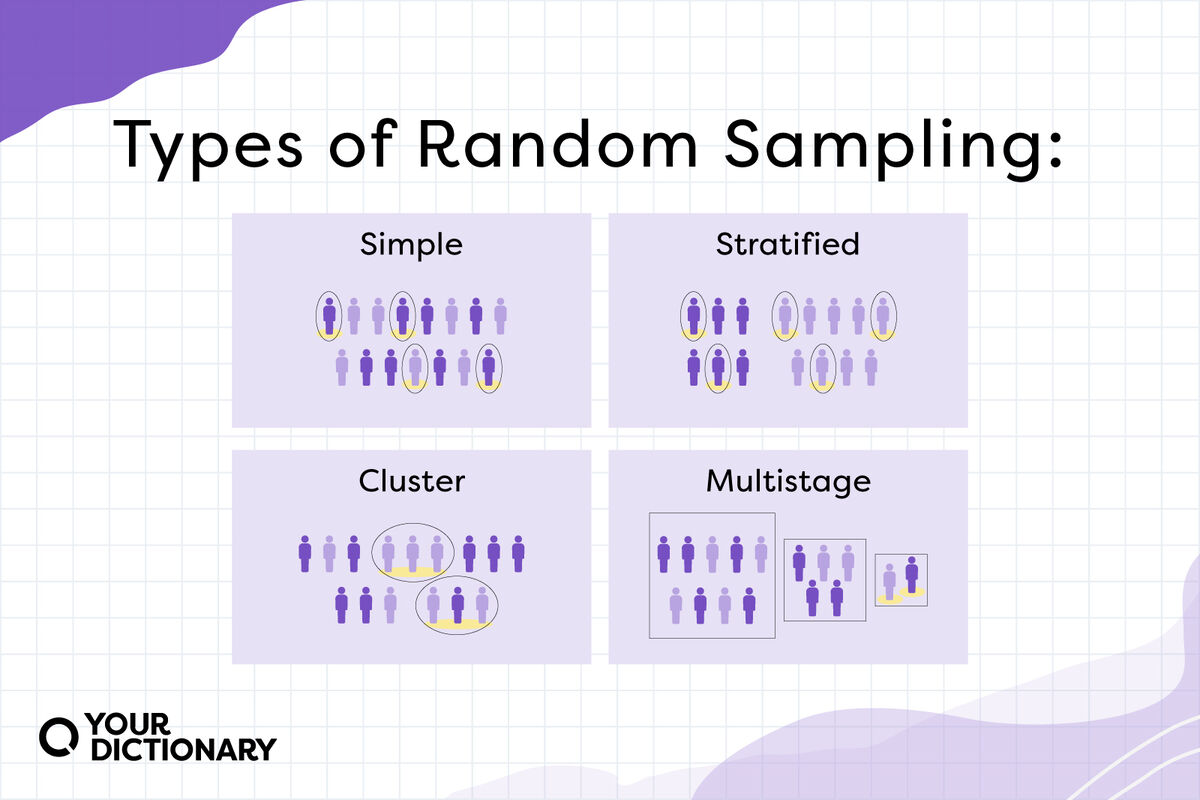
Types of Random Sampling
Methodology is vital to getting a truly random sample. Use an imperfect method and you risk getting biased or nonsensical results. The following are commonly used random sampling methods:
- Simple random sampling
- Stratified random sampling
- Cluster sampling
- Multistage sampling
Each of these random sampling techniques are explained more fully below, along with examples of each type.
Random sampling uses specific words for certain things. "Population" means every possible choice. Whether you're choosing numbers, things or people, "population" means "all the possible things I could choose." "Sample," logically enough, means the thing or things you choose from the population to study.
Simple Random Sampling
As you'd guess by the name, this is the most common approach to random sampling. Simple random sampling means simply to put every member of the population into one big group, and then choosing who or what to include at random. As long as every possible choice is equally likely, you will produce a simple random sample.
Real world examples of simple random sampling include:
- At a birthday party, teams for a game are chosen by putting everyone's name into a jar, and then choosing the names at random for each team.
- On an assembly line, each employee is assigned a random number using computer software. The same software is used periodically to choose a number of one of the employees to be observed to ensure they are employing best practices.
- A restaurant leaves a fishbowl on the counter for diners to drop their business cards. Once a month, a business card is pulled out to award one lucky diner with a free meal.
- At a bingo game, balls with every possible number are placed inside a mechanical cage. The caller rotates the cage, tumbling around the balls inside. Then, she selects one of the balls at random to be called, like B-12 or O-65.
- A pharmaceutical company wants to test the effectiveness of a new drug. Volunteers are assigned randomly to one of two groups. The first group will receive the new drug; the second group will receive a placebo.
Stratified Random Sampling
In stratified random sampling, the population is divided into groups based on a shared characteristic. Each group is called a stratum; the plural is strata. Then, one or more choices are made at random from each stratum.
- A survey about timekeeping might divide the population by time zone, then take 100 random samples per zone.
- A test addressing physical development over time could use the student body of a school as a population, stratify it by grade, and then take random samples from each grade.
- A study on tax reform might stratify a population according to income, then take random samples from each stratum.
- Opinion surveys on specific political issues commonly stratify according to respondents' party affiliation (or lack thereof), then take samples from each.
- A market survey by a company interested in branching into a new market might choose a population of people using similar products, stratify it by brand, and sampling from each stratum.
Cluster Sampling
Cluster sampling is similar to stratified random sampling in that both begin by dividing the population into groups based on a particular characteristic. But, while a stratified survey takes one or more samples from each of the strata, a cluster sampling survey chooses clusters at random, then takes samples from them. Some clusters aren't sampled; data is only collected from the chosen clusters. Cluster sampling is often used in market research.
- A study in the wake of a natural disaster might divide a population into clusters according to region, then choose a random cluster or clusters to begin establishing the disaster's overall effect.
- A company interested in brand penetration may lack the resources to survey an entire city. Instead, they could divide the city into clusters based on area, choose clusters at random, and test the popularity of their brand. This is also how some mail campaigns are conducted.
- A test of the effectiveness of a new curriculum could begin by dividing an area by school district, then choosing a school or set number of schools at random and sampling students from each.
- Data relating to universal phenomena is often obtained by cluster sampling. Take the example of a statewide survey testing the average resting heart rate. The state could divide into clusters based on counties, then choose counties at random to test.
- A survey assessing customer satisfaction with a product might establish clusters based on place of purchase, then choose a number of those clusters at random.
Multistage Sampling
Multistage sampling is exactly what it says on the label: a sampling process that uses more than one kind of sampling.
- The same business referenced above, the one that used cluster sampling to study brand penetration, might break down the neighborhood clusters into strata according to income and take a simple random sample from each subgroup.
- Likewise, after establishing clusters based on area, the natural disaster survey might stratify each according to age before selecting samples in order to determine any disproportionate effect based on age.
- A test tracking physical development in students over time might begin with cluster sampling by district, selecting one specific school at random. They might then stratify according to age and gender before taking simple random samples.
- Local government testing a possible new policy might divide its jurisdiction into random clusters based on area, then stratify those clusters by party affiliation.
- A charity tracking the occurrence of a particular illness might create random clusters that cover all affected areas, then choose one and stratify it by percentage of affected people, testing only those strata above a certain percentage.
-
Get Random
The importance of random sampling is hard to overstate. Scientific testing relies on it. Governments, businesses and charities depend on it. Anyone who systematically collects information about how the world works is likely to need a truly random sample at some point.
To continue improving your mathematical and scientific rigor, take a look at our examples of control groups.