Pauli-vector Definition
noun
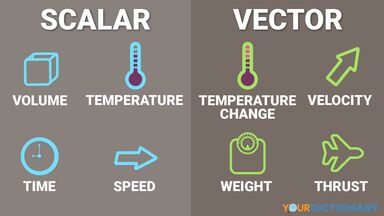
(mathematics) A vector whose components are Pauli matrices; e.g..
The eigenvectors of the first Pauli matrix "encode" — as it were — the +X and −X directions. Likewise, the eigenvectors of the second Pauli matrix "encode" the +Y and −Y directions and those of the third Pauli matrix, the +Z and −Z directions. The dot product of the Pauli vector with any unit vector yields a matrix which likewise has eigenvalues +1 and −1 and a pair of eigenvectors; the eigenvector with positive eigenvalue "encodes" the +N direction and the eigenvector with negative eigenvalue "encodes" the −N direction. The dot product of any two such "encoded" directions yields the probability amplitude that the spin of an electron prepared in the first direction will collapse to the second direction when measured along that second direction.
Wiktionary
Related Articles
Find Similar Words
Find similar words to pauli-vector using the buttons below.