Euler-s-totient-function Definition

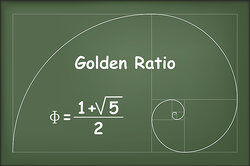
Due to Euler's theorem, if f is a positive integer which is coprime to 10, then where is Euler's totient function. Thus , which fact which may be used to prove that any rational number whose expression in decimal is not finite can be expressed as a repeating decimal. (To do this, start by splitting the denominator into two factors: one which factors out exclusively into twos and fives, and another one which is coprime to 10. Secondly, multiply both numerator and denominator by such a natural number as will turn the first said factor into a power of 10 (call it N). Thirdly, multiply both numerator and denominator by such a number as will turn the second said factor into a power of 10 minus one (call it M). Fourthly, resolve the numerator into a sum of the form . Then the repeating decimal has the form where b may be padded by zeroes (if necessary) to take up digits, and c may be padded by zeroes (if necessary) to take up digits.)